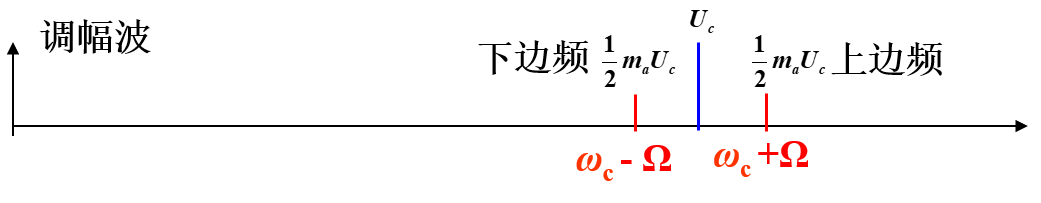AM调制
定义
AM调制是指用调制信号的幅度来调制载波信号的一种调制方式。AM调制的数学表达式为:
$$ s(t) = (1 + m(t)) \cdot \cos(2\pi f_c t + \theta) $$
其中,$m(t)$为调制信号,$f_c$为载波频率。一般的,对于正弦调制的AM信号,AM信号$s(t)$为:
$$ s(t) = (1+m_a\cdot \cos(2\pi f_m t +\varphi)) \cdot \cos(2\pi f_c t +\theta) $$
其中,$m_a$ 为调制信号的幅度,也称为调制系数,$f_m$为调制信号的频率,$f_c$ 为载波频率,$\varphi$ 为调制信号的相位,$\theta$ 为载波信号的相位。
AM信号的生成
可使用如下的MATLAB代码生成AM信号:
fc = 2e6; % 2M载波
fm = 1e3;
fs = 24e6;
ma = 0.5;
t = 0:1 / fs: 65535 / fs;
% Modulation
mt = cos(2 * pi * fm * t);
ct = 0.05 * cos(2 * pi * fc * t);
st = (1 + ma * mt) .* ct;
% Plot Modulation Signal
plot(t,st)
AM信号的频谱
不妨令载波和调制信号的初相位均为0,即 $\theta = \varphi = 0$,则AM信号的表达式为:
$$ s(t) = (1+m_a\cdot \cos(2\pi f_m t)) \cdot \cos(2\pi f_c t) $$
使用和差化积公式,可将AM信号的表达式化为:
$$ \cos(\omega_c t)+\frac{m_a}{2}\cos((\omega_c+\omega_m)t)+\frac{m_a}{2}\cos((\omega_c-\omega_m)t) $$
对应的频谱为:
$$ \frac{1}{2}\delta(\omega-\omega_c)+\frac{m_a}{4}\delta(\omega-\omega_c-\omega_m)+\frac{m_a}{4}\delta(\omega-\omega_c+\omega_m)+\frac{1}{2}\delta(\omega+\omega_c)+\frac{m_a}{4}\delta(\omega+\omega_c-\omega_m)+\frac{m_a}{4}\delta(\omega+\omega_c+\omega_m) $$
AM信号的调制度
从AM信号的定义式上可以看出,调制度即基带调制信号的幅度除以叠加在基带调制信号上的直流偏置,取值范围为 $[0,1]$。调制度越大,AM信号的动态范围越大,但是带宽也会增大。当 $m_{a}$ >1时,AM信号会出现过调制现象,此时会出现信号失真。
需要测量AM信号的调制度时,可以在示波器上使用光标测量AM信号的波峰和波谷的电压,然后计算调制度:
$$ m = \frac{V_{max}-V_{min}}{V_{max}+V_{min}} $$
也可以使用示波器的FFT功能,选择合适的窗函数与频率范围,测量AM信号的频谱,然后计算调制度:
$$ m = 2\cdot 10^{\frac{A_{w_c}-A_{w_c\pm w_m}}{20}} $$
其中,$A_{w_c}$ 为载波频率的幅度,$A_{w_c\pm w_m}$ 为载波频率的两个相邻的频率分量的幅度,均以dB为单位。
补充:将信号数据导入Matlab后,可以使用如下代码计算AM信号的调制度:
data = csvread('data.csv');
data = data - mean(data);
% 寻找极大值(波峰)
maxPeak = findpeaks(data);
% 寻找极小值(波谷)
minPeak = -findpeaks(-data);
% 计算调制度
m = (maxPeak - minPeak) / (maxPeak + minPeak);
AM解调
AM信号的解调方式有很多种,大体上可以分为同步检波(相干解调)和包络检波(非相干解调)两种方式。
同步检波
同步检波是指将AM信号与载波信号相乘,然后通过低通滤波器滤除高频分量,得到原始的调制信号。同步检波的数学表达式为:
$$ \begin{aligned} m(t) &= s(t) \cdot \cos(2\pi f_c t +\varphi) \\ &= (1+m_a\cdot \cos(2\pi f_m t)) \cdot \cos(2\pi f_c t) \cdot \cos(2\pi f_c t+\varphi) \\ &= \frac{1}{2}\cos(\varphi)+\frac{m_{a}}{2}\cos(2\pi f_m t)\cos(\varphi)+\frac{1}{2}\cos(4\pi f_c t+\varphi)+\frac{m_{a}}{2}\cos(2\pi f_m t)\cos(4\pi f_c t+\varphi) \end{aligned} $$
其中,$m(t)$ 为解调后的调制信号,$\varphi$ 为载波信号的相位。
使用一个低通滤波器,可以滤除高频分量,再通过去直流处理后,即可得到原始的调制信号。
当 $\varphi$ 取值不合适时,会影响解调信号的幅值
包络检波
数字包络检波
数字包络检波是指将AM信号取绝对值后,通过一个低通滤波器进行解调,数学推导如下:
$$ \begin{aligned} m(t) = |s(t)| &= |(1+m_a\cdot \cos(2\pi f_m t)) \cdot \cos(2\pi f_c t)| \\ &=(1+m_a\cdot \cos(2\pi f_m t))\cdot |\cos(2\pi f_c t)|\\ &=(1+m_a\cdot \cos(2\pi f_m t))\cdot \cos(2\pi f_c t)\cdot f(t)\\ &=s(t)\cdot f(t) \end{aligned} $$
其中,$f(t)$ 为周期方波信号,$f(t)$ 的表达式为:
$$ f(t) = \left\{ \begin{aligned} 1, \quad -\frac{\pi}{2}+2k\pi<&\omega_c t<\frac{\pi}{2}+2k\pi \\ -1, \quad \frac{\pi}{2}+2k\pi<&\omega_c t<\frac{3\pi}{2}+2k\pi \end{aligned} \right. $$
当取绝对值后,信号的频谱会发生变化,由傅里叶变换的性质可知:
$$ \mathscr{F}\{|s(t)|\} = \mathscr{F}\{s(t)f(t)\}=\frac{1}{2\pi}\cdot\mathscr{F}\{s(t)\}*\mathscr{F}\{f(t)\} $$
$s(t)$ 的频谱我们在上面已经计算过,下面来计算 $f(t)$ 的频谱,$f(t)$ 为连续周期方波信号,这里先计算其傅里叶级数:
$$ \begin{aligned} a_k &= \frac{\omega_c}{2\pi}\int_{-\frac{\pi}{\omega_c}}^{\frac{\pi}{\omega_c}}f(t)e^{-jk\omega_c}dt \\ &= \frac{\omega_c}{2\pi}\left(\int_{-\frac{\pi}{\omega_c}}^{-\frac{\pi}{2\omega_c}}-e^{-jk\omega_c}dt+\int_{-\frac{\pi}{2\omega_c}}^{\frac{\pi}{2\omega_c}}e^{-jk\omega_c}dt+\int_{\frac{\pi}{2\omega_c}}^{\frac{\pi}{\omega_c}}-e^{-jk\omega_c}dt\right)\\ &= \frac{2 \sin{\left(\frac{\pi k}{2} \right)} - \sin{\left(\pi k \right)}}{\pi k}\\ &= \frac{2 \sin{\left(\frac{\pi k}{2} \right)}}{\pi k}\\ \end{aligned} $$
由连续周期信号的频谱性质可知,$f(t)$ 的频谱为:
$$ \begin{aligned} \mathscr{F}\{f(t)\}=F(\omega) &= \sum_{k=-\infty}^{\infty}2\pi a_k\delta(\omega-k\omega_c) \\\\ &= \sum_{k=-\infty}^{\infty}\frac{4 \sin{\left(\frac{\pi k}{2} \right)}}{ k}\delta(\omega-k\omega_c) \end{aligned} $$

进一步的,我们可以计算 $|s(t)|$ 的频谱:
$$ \begin{aligned} \mathscr{F}\{|s(t)|\} &= \frac{1}{2\pi}\cdot\mathscr{F}\{s(t)\}*\mathscr{F}\{f(t)\} \\ &= \frac{1}{2\pi}\left(\frac{1}{2}\delta(\omega-\omega_c)+\frac{m_a}{4}\delta(\omega-\omega_c-\omega_m)+\frac{m_a}{4}\delta(\omega-\omega_c+\omega_m)+\frac{1}{2}\delta(\omega+\omega_c)+\frac{m_a}{4}\delta(\omega+\omega_c-\omega_m)+\frac{m_a}{4}\delta(\omega+\omega_c+\omega_m)\right)*F(\omega)\\ &=\frac{1}{2\pi}\left(\delta(\omega)+\frac{1}{2}\delta(\omega+2\omega_c)+\frac{1}{2}\delta(\omega-2\omega_c)+\frac{m_a}{4}\delta(\omega-\omega_m)+\frac{m_a}{4}\delta(\omega+\omega_m)+\frac{m_a}{4}\delta(\omega-2\omega_c-\omega_m)+\frac{m_a}{4}\delta(\omega-2\omega_c+\omega_m)+ \cdots \right) \end{aligned} $$
我们只需要设计一个通带频率大于$\omega_m$,阻带频率小于 $2\omega_m$的低通滤波器,将高频分量滤除,再去除直流量即可得到原始的调制信号。
以上述24MHz采样率,2MHz载波,1KHz的AM信号为例,我们可以使用如下代码对AM信号进行包络检波:
clear,clc,close all;
fc = 2e6; % 2M Carrier
fm = 1e3; % 1KHz Modulation
fs = 24e6;
ma = 0.5;
t = 0:1 / fs:65535 / fs;
% Modulation
mt = cos(2 * pi * fm * t);
ct = 0.05 * cos(2 * pi * fc * t);
st = (1 + ma * mt) .* ct;
% Envelope Detection
st_abs = abs(st);
% Low Pass Filter
Rp = 1; % Passband Ripple
Rs = 80; % Stopband Attenuation
% Normalized Frequency
Wp = 1.2 * fm / (fs / 2); % Passband Edge
Ws = 0.9 * 2 * fc / (fs / 2); % Stopband Edge
% Filter Design
d = fdesign.lowpass('Fp,Fst,Ap,Ast', Wp, Ws, Rp, Rs);
Hd = design(d, 'equiripple');
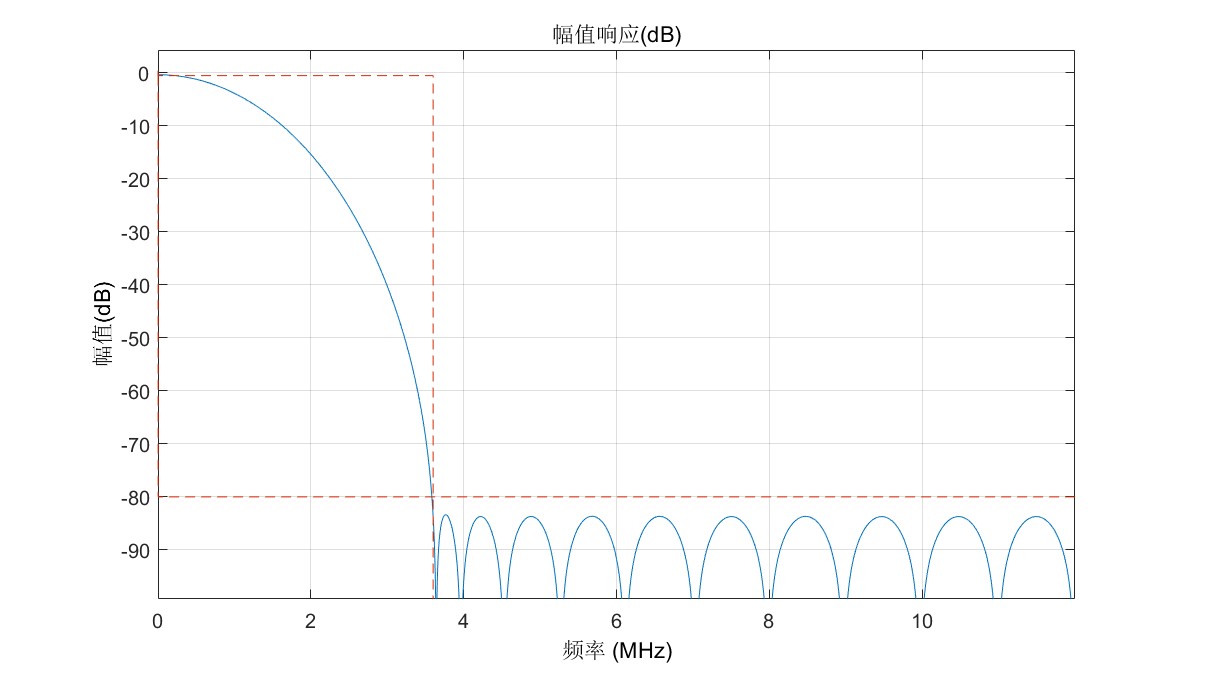
% Frequency Response
freqz(Hd)
% Filter Signal
st_filt = filter(Hd, st_abs);
% Remove DC
st_filt = st_filt - mean(st_filt);
% Plot
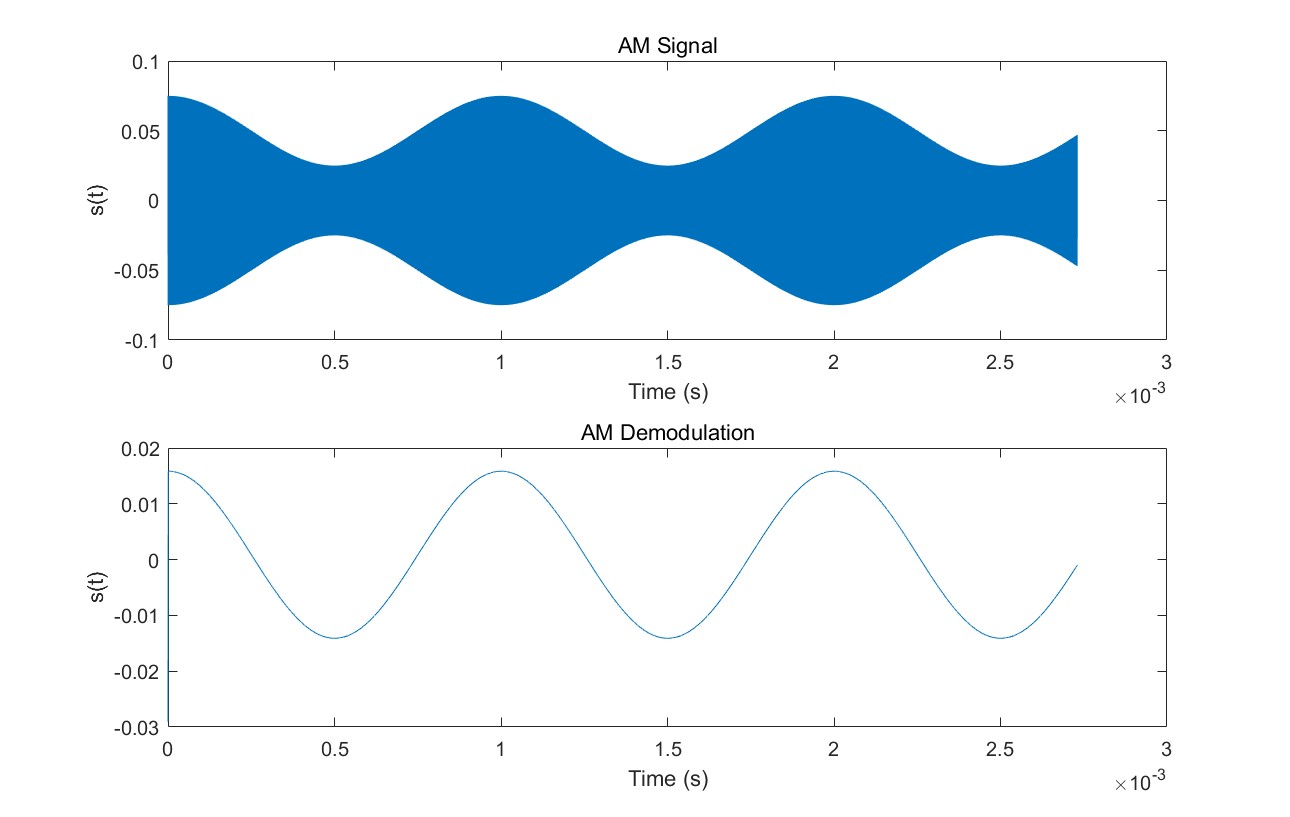
figure;
subplot 211;
plot(t, st);
xlabel('Time (s)');
ylabel('s(t)');
title('AM Signal');
subplot 212;
plot(t, st_filt);
xlabel('Time (s)');
ylabel('s(t)');
title('AM Demodulation');
模拟包络检波
使用如下图所示的二极管检波电路可实现对AM信号的检波: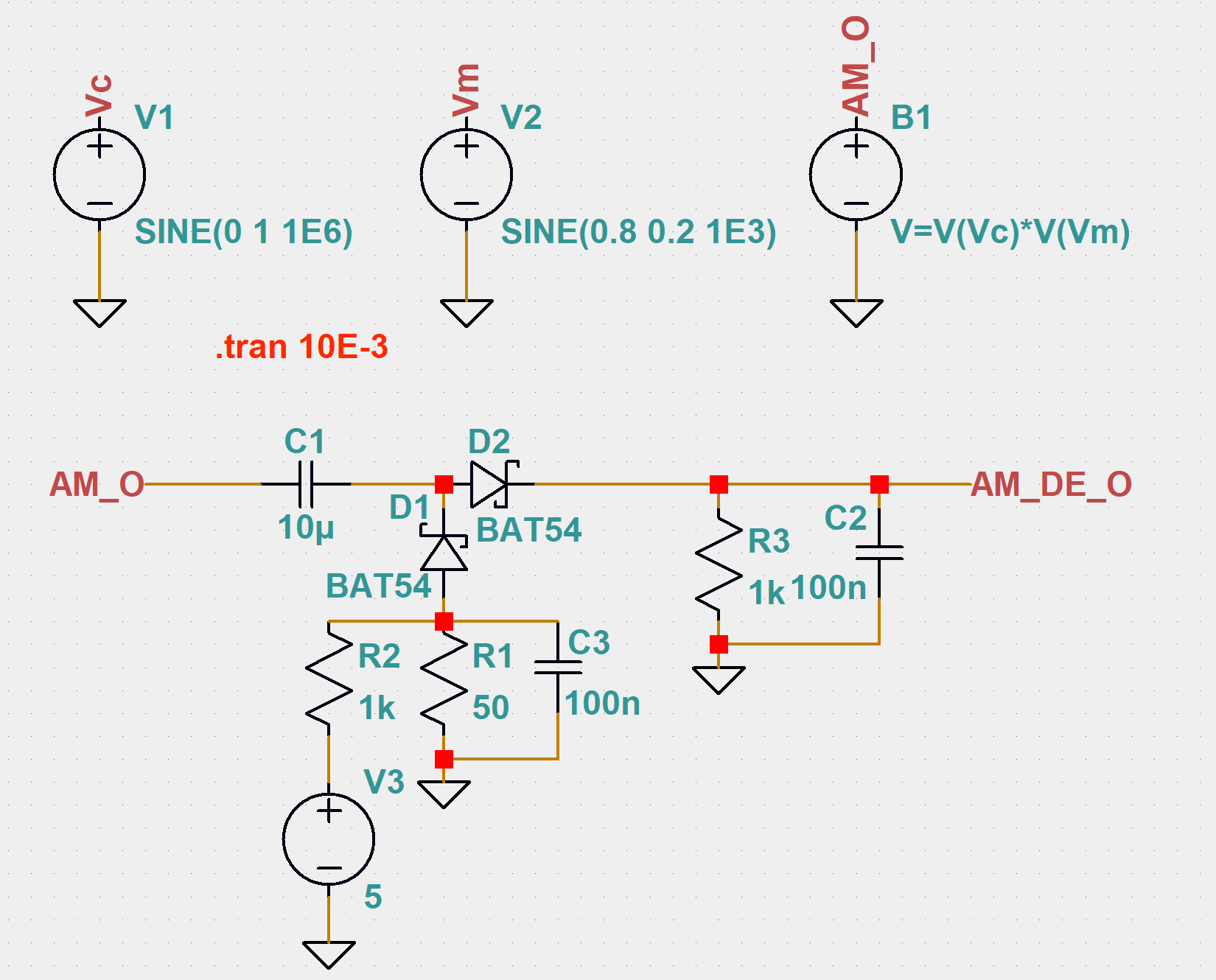
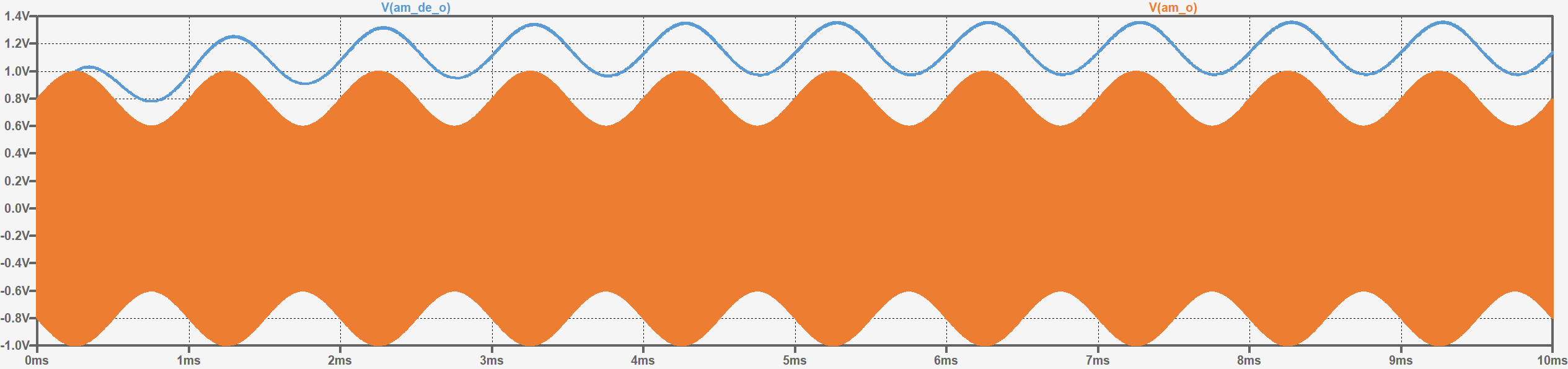
两种检波方式的比较
- 同步检波:
- 优点:适用范围广阔,能够用于多种调制信号。包括且不限于AM信号。
- 缺点:需要用到乘法器以及DDS,解调装置较为复杂,成本较包络检波高,
- 包络检波:
- 优点:模拟包络检波器简易并且经济,数字包络检波器实现思路较为简单
- 缺点:仅能够解调调制系数大于等于1的AM信号,适用范围窄